I said a few weeks ago that I was going to talk more about this article by Chris Olah and Shan Carter on the idea of research debt, but every time I went back to it I felt that the original article made the point so clearly and elegantly that there was very little I wanted to add. (Other than ‘I want this thing in physics too please!’)
So I started to pull out my favourite bits, intending to do a very lazy quotes-and-comments sort of post, and realised that with a couple of additions they made a coherent summary of the original post on their own. In the process I discovered that there were a few things I wanted to say, after all.
If you just read straight down the blockquotes you get a double-distilled microversion of the original essay. Or you can also read the bits I’ve stuck in between.
For centuries, countless minds have climbed the mountain range of mathematics and laid new boulders at the top. Over time, different peaks formed, built on top of particularly beautiful results. Now the peaks of mathematics are so numerous and steep that no person can climb them all.
This has always saddened me. In Men of Mathematics, E. T. Bell labels Henri Poincaré as the ‘The Last Universalist’, the last person to be able to range freely across all fields of mathematics as they existed in his time. Now Bell did have a tendency to over-dramatise things, but I think this is basically right.
Probably this is unavoidable; probably the expansion wave has accelerated too fast, and those days will not return. I’m temperamentally susceptible to millenarian dreams of the return of the once and future universalists, but I accept that this is unlikely.
Still, there is a lot of compression that is within reach:
The climb is seen as an intellectual pilgrimage, the labor a rite of passage. But the climb could be massively easier. It’s entirely possible to build paths and staircases into these mountains. The climb isn’t something to be proud of.
The climb isn’t progress: the climb is a mountain of debt.
The analogy is with technical debt in programming, which is all the awkward stuff thrown to the side in an effort to get software into production quickly. Eventually you have to go back and deal with the awkward stuff, which has an unfortunate tendency to compound over time.
The insidious thing about research debt is that it’s normal. Everyone takes it for granted, and doesn’t realize that things could be different. For example, it’s normal to give very mediocre explanations of research, and people perceive that to be the ceiling of explanation quality. On the rare occasions that truly excellent explanations come along, people see them as one-off miracles rather than a sign that we could systematically be doing better.
People who are truly excellent at explaining research are probably rare. But ‘better explanations than we have currently’ seems like a very, very easy target to hit, once people are persuaded to put resources into hitting it.
I plan to finally start taking my own advice soon, and start putting whatever notes and bits of intuition I’ve gathered online. I’m not too convinced that they’ll be especially great, but the current floor is pretty low.
Research distillation is the opposite of research debt. It can be incredibly satisfying, combining deep scientific understanding, empathy, and design to do justice to our research and lay bare beautiful insights.
Distillation is also hard. It’s tempting to think of explaining an idea as just putting a layer of polish on it, but good explanations often involve transforming the idea. This kind of refinement of an idea can take just as much effort and deep understanding as the initial discovery.
Distillation is fundamentally a different sort of activity to the types of research that are currently well supported by academia. Distillers aren’t mountain climbers; they engage with their subject by criss-crossing the same ground over and over again, following internally-generated trails of fascination that can be hard to interpret from the outside. They want to understand!
An aspiring research distiller lacks many things that are easy to take for granted: a career path, places to learn, examples and role models. Underlying this is a deeper issue: their work isn’t seen as a real research contribution. We need to fix this.
Distillers generally have little interest in who can get to the top of the mountain fastest, and anyway it certainly won’t be them. In an environment that rewards no other activity, they tend to disappear quickly. They require different infrastructure.
None of this infrastructure currently exists, but it easily could do. Research distillation doesn’t intrinsically need to cost huge amounts of money. It’s not like we need to spend billions on a gigantic high-energy collider to smash our current explanations together. This is an area where transitioning from moaning about academia to actually doing something about it looks to be pretty straightforward.
It’s one of the nice sorts of problems where small efforts at the margins are already useful. It certainly helps if you have Google’s resources behind you, but you can also just polish up any half-decent notes you have lying around on a topic that’s currently poorly explained and put them online, and you’ve made a tiny contribution towards fixing the problem.
If you are excited to distill ideas, seek clarity, and build beautiful explanations, we are letting you down. You have something precious to contribute and we aren’t supporting you the way we should.
I’ve been saying ‘they’ throughout this post, but, I mean, it’s obvious why I care about this thing. This is my old tumblr ‘about me’ page:
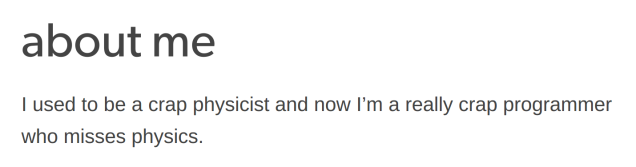
It’s amusing self-deprecation, but unfortunately I also meant it a lot of the time. (I still believe the programmer bit, but I’m starting to have some optimism about improvement there too.) My standard line after finishing my thesis was ‘I love physics but I’m bad at research’.
I had a poorly understood but strongly felt sense of what I wanted instead, academia was clearly not going to provide it, and I just wanted to get out. ‘Research distillation’, however, is a reasonably close fit. (Maybe not an exact one. I feel the ‘criss-crossing existing territory’ approach goes deeper than just refining existing ideas, and is a valid route to original research in itself. But it’s an ecosystem I think I would have been able to cope with, and succeed in.)
So I’ll admit my enthusiasm for the idea of research distillation is mostly pure self-interest. But I’m pretty sure that a thriving ecosystem of distillers would also help academia. After all, you only criss-cross the territory for love of the subject. The external rewards are currently too poor for any other motivation to make sense.
This post series might be relevant: https://betterexplained.com/articles/developing-your-intuition-for-math/
It’s aiming at early undergraduate level math, and you’re interested in more advanced stuff, but its explanations of mathematical intuition seem good. (Although I’ve read only a bit of it.)
I learned about this because Kevin Simler pointed me at the “ADEPT method” post (about halfway through the series.)
LikeLike
Ah cool, thanks! That site’s excellent – I’ve looked at a few specific explanations on there, but hadn’t seen that particular series. Will give it a read.
Early undergrad is a great level to target because that’s so often where it goes wrong for people (certainly it was a big shock for me as I’d had excellent teaching before that). Linear algebra, complex analysis and multivariable calculus are inherently visual topics, but often rushed through, so students get left with a very fragile, rote-calculation-based understanding.
I am mostly interested in somewhat more advanced maths though, something like late undergrad/grad school taught course level. Particularly ‘physicist’s maths’ – differential geometry, Lie groups and algebras, and the sort of stuff you get in mathematical methods textbooks (a lot of this is really pretty, but mostly gets taught as a box of arbitrary tricks). Basically the stuff I’m still trying to grasp intuitively myself, though I know that I still have big holes to fill at the early undergrad level too.
A lot of this could be taught earlier if it was digested better and presented in the right form. E.g. there’s this fantastic little book on differential forms: https://arxiv.org/abs/math/0306194v1 Probably the only book aimed at second year engineering students with an appendix on de Rham cohomology!
(Just looked at your Twitter account too btw… that logic book intro you retweeted looks good. I’m getting tempted to get an account despite my ambivalence about Twitter, as you all seem to post really interesting stuff!)
LikeLiked by 1 person
I’ve read more of that insight series now, there’s some excellent stuff there.
Sort of related: that Writing Process graph you retweeted from the Ribbonfarm course is spot on for understanding maths as well (though I also like writing on the ‘too early’ upslope). I often feel kind of guilty when I look at stuff like Better Explained, because I mostly don’t put much effort into explaining intuition once I’ve got it myself. It suddenly passes into ‘obvious’/’boring’/’maybe everyone else already secretly knows this and I’m the sole idiot’ territory, and writing it then feels unpleasant.
But I like the idea of catching ideas at the top of the graph, so there’s genuine excitement rather than a sense of duty… And now that I’ve thought about it, I realise Kalid Azad started writing that site *while* he was a student figuring out all those ideas himself, which is probably why he’s still excited to explain them!
LikeLiked by 1 person
Many things get discovered multiple times but its the person who explains it better who gets the fame. If you’re willing to post things as you distill them for yourself I will read everything you write.
LikeLike
I do plan to start doing that soon! Probably on a different site to here, but I will link to it from here.
LikeLike
I feel very similarly to you, and I often wonder if this stance is why I’m attracted to category theory. It seems like category theory produces a simple distilled “core” when applied to different fields/constructions, and the idea of “categorification” seems analogous to distillation in a way.
LikeLike
Yes this seems plausible! I haven’t got the category theory bug yet, but some of the other people I meet who are into foundations of physics really have.
It’s quite hard for me personally to get into, because my own orientation is always to go from concrete to abstract, and category theory is very much at the abstract end of things. Also my algebra background is somewhat weak. But maybe eventually I’ll build up enough of a repertoire of concrete examples that I’ll finally be able to abstract my way up to it and get the point 🙂
LikeLike